3D그래픽스 - 회전(Rotation) ::: Sevity Blog

3D그래픽스 - 회전(Rotation)

2019. 1. 9. 14:14

좌표계

직교좌표계(Cartesian coordinate system)

(x,y,z) 뻔한거

구면좌표계(spherical coordinate system)

반지름, 위도, 경도 $(r,\theta ,\phi )$

Rotation

Euler angle(오일러각)

3차원 벡터의 방향을 세 개의 각으로 표시한 것

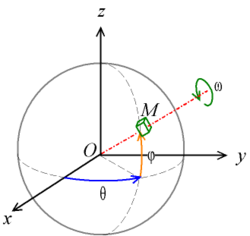
위에서 물체 M이 놓인 방향을 (α, β, γ) 또는 (ψ, θ, φ)로 표현

x,y,z축에 대해서 회전하는 쉬운 개념이 tait-bryan angle이고 proper Euler angle은 좀 어렵다 x,y,z가 아니라 z,x,z 이런식으로 회전한다는데 정확히 이해 못함

또한 Intrinsic vs Extrinsic rotations 개념이 있다.

전자는 회전축이 변경되는거고 후자는 고정.

처음회전은 둘다동일한데 다음회전을 다른축에 대해서 할때 전자는 첫번째 회전에 의해 이동된 축을 기준으로 회전하고 후자는 원래부터 고정된 월드회전축 기준으로 회전함

Axis-angle representation

Rotation matrix

2차원일때

$R={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}$

원점(0,0)을 기준으로 반시계방향(오른손 좌표계)으로 회전하는 행렬은 위와 같다.

특정한 픽셀의 좌표가 컬럼벡터 v로 표현될때 해당 필셀을 회전한 후의 좌표는 형렬연산으로 Rv 가 된다.

${\begin{bmatrix}x'\\y'\\\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}{\begin{bmatrix}x\\y\\\end{bmatrix}}$

3차원일때

2차원 회전에서는 회전축이 가상의 z축 하나라면 3차원 회전에서는 회전에 대해 고를 수 있는 축이 3개가 된다(x축, y축, z축)

각각에 대해서 오른손 좌표계(축을 오른손 엄지로 놓았을때 나머지 네 손가락이 쥐어지는 방향..반시계) 기준으로 회전행렬은 다음과 같다.

${\begin{alignedat}{1}R_{x}(\theta )&={\begin{bmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\[3pt]0&\sin \theta &\cos \theta \\[3pt]\end{bmatrix}}\\[6pt]R_{y}(\theta )&={\begin{bmatrix}\cos \theta &0&\sin \theta \\[3pt]0&1&0\\[3pt]-\sin \theta &0&\cos \theta \\\end{bmatrix}}\\[6pt]R_{z}(\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta &0\\[3pt]\sin \theta &\cos \theta &0\\[3pt]0&0&1\\\end{bmatrix}}\end{alignedat}}$

2차원 회전행렬과 상당히 비슷한걸 볼 수 있다.

재밌는점은

저작자표시

'수학' 카테고리의 다른 글

직교행렬(orthogonal matrix) (0)	2019.01.09
고유값, 고유벡터(eigenvalue and eigenvector) (0)	2019.01.09
likelihood(가능도 = 우도) (0)	2018.10.02
MLE, 최대우도추정(Maximum Likelihood Estimation) (0)	2018.09.27
베이즈 정리(Bayes' theorem) (0)	2018.09.27

Sevity Blog