베타분포 개념: 베르누이 확률 추정과 베타함수

베타분포는 0과 1 사이의 확률값 자체를 모델링할 때 자주 쓰이는 분포다. 베르누이 시행의 성공 확률처럼 알 수 없는 파라미터를 추정하는 상황에서 베이즈 관점으로 이해하기 좋다.

이 글은 베르누이분포의 파라미터 추정, 사전확률과 사후확률, 베타함수, 감마함수, 조합과의 관계, 베타분포의 정규화 직관을 정리한 메모다.

 

핵심 정리

베르누이 시행에서는 결과가 성공 또는 실패로 나뉘고, 우리가 알고 싶은 값은 성공 확률 같은 파라미터다. 관측 데이터가 주어졌을 때 어떤 파라미터가 더 그럴듯한지 보려면 베이즈 정리의 사전확률, 가능도, 사후확률 관점으로 생각할 수 있다. 베타분포는 0과 1 사이에서 정의되는 확률값을 표현하기 좋아서 베르누이 성공 확률의 사전분포나 사후분포를 다룰 때 자주 등장한다. 베타함수는 베타분포가 전체 확률 합이 1이 되도록 만드는 정규화 상수의 역할로 볼 수 있다. 원문처럼 감마함수와 조합을 함께 보면, 자연수 조합에서 실수 범위로 확장되는 감각을 잡는 데 도움이 된다.

• 베타분포는 0과 1 사이의 확률 파라미터를 표현할 때 유용하다.
• 베르누이분포에서는 성공 확률 같은 파라미터를 추정하는 문제가 생긴다.
• 사전확률은 데이터를 보기 전 파라미터에 대한 믿음이다.
• 가능도는 특정 파라미터에서 관측 데이터가 나올 그럴듯함이다.
• 사후확률은 관측 데이터를 본 뒤 갱신된 파라미터 분포다.
• 베타함수는 베타분포를 확률분포로 만들기 위한 정규화 역할을 한다.
• 감마함수는 팩토리얼을 더 넓은 범위로 확장해 보는 데 쓰인다.
• 베타분포는 성공과 실패 횟수가 쌓일수록 모양이 바뀌는 직관을 준다.

원문은 베타분포를 베르누이 파라미터 추정과 베이즈 정리 관점에서 이해하려는 수학 메모입니다. 보강문에서는 수식을 새로 늘리지 않고, 사전확률, 가능도, 사후확률, 베타함수의 역할을 분리했습니다. 베타분포는 공식보다 확률값 자체에 대한 분포라는 점을 먼저 잡으면 훨씬 덜 낯섭니다.

여기 참조

직관

베타분포는 베르누이분포의 모수(모델 또는 파라미터) $\theta$를 추정하는데 쓰인다.

동전던지기를 예로 들면 베르누이 분포는 다음과 같이 되는데..

$$p(y|\theta) = \theta^y(1-\theta)^{(1-y)}$$

우리가 궁금한것은 모델이 주어졌을때의 샘플의 확률이 아니라, 거꾸로 샘플이 주어졌을때 어떤 모델($\theta$)이 적합한가이기 때문에, (ML적인 관점에선 당연하고 학습과정이 곧 이것)

거꾸로 $p(\theta|y)$에 관심이 있고 구해야하는 값이다.

그런데 베이즈 정리에 따르면 

$P(\theta|y) = {{P(y|\theta)P(\theta)}\over{P(y)}}$가 되고, 다음과 같은 의미로 해석한다.

$$사후확률(posterior) = {{가능도(likelihood) \times 사전확률(prior)}\over{증거(evidence)}}$$

즉 우리가 학습을 한다는 것은 사후확률을 구한다고도 얘기할 수 있는데, 이때 베타함수 형태로 가정하면 식을 세우기 편하다고 직관적으로 보면 딱 좋을것 같다.

(즉 무조건 사후확률이 베타분포가 된다는게 아니라 베타분포로 가정한다는걸 이해하는게 중요)

베타함수

베타함수는 두변수(x, y)에 대한 다변수 함수이며 다음과 같이 정의된다.

x>0, y>0일때

$$B(x, y) = \int_0^1 t^{x-1}(1-t)^{y-1}dt$$

보통 팩토리얼이 감마함수로 일반화 되듯이,

조합(Combination)의 일반화로 이야기 된다.

조합은 이항계수라고도 하고 n과 k가 자연수일때 다음과 같이 정의된다.

$$_nC_k = {n \choose k} = {{n!}\over{k!(n-k)!}}$$

보면 자연수일때도 팩토리얼이 들어가므로, 실수, 복소수로 확장하게 된다면 감마함수가 들어가는게 자연스러울 거란걸 알 수 있다.

베타함수는 감마함수를 쓰면 다음과 같이 된다.

$$B(x,y) = {{\Gamma(x)\Gamma(y)}\over{\Gamma(x+y)}}$$

근데 위 식을 보면은 감마함수의 경우는 팩토리얼과 아주 유사하게 되어 있는데 이항계수식과 베타함수를 보면 분모분자도 바뀌어 있는것 같고 뭔가 정확히 같아보이진 않는다.

실제로 m과n이 자연수일때 둘간의 관계를 나타내 보면 다음과 같이 서로 역수 형태임을 알 수 있다.

$$B(m,n) = {1\over{m\cdot _{m+n-1}C_{n-1}}}$$

$${n \choose k} = {1\over{(n+1)B(n-k+1,k+1)}}$$

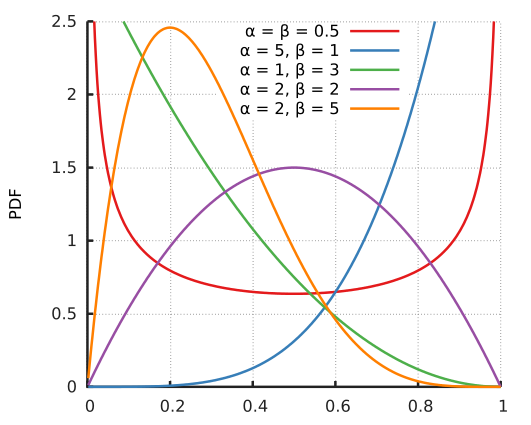
베타분포

역시나 감마함수가 감마분포가 될 때와 마찬가지로 적분값을 1.0으로 만들기위해 역수로 나눠주는 과정이 들어가 있다.

 

$\alpha, \beta$에 따른 분포의 모양은 위와 같다.