여기 참조함
아래처럼 그래프에서 사이클을 제거하고 트리형태로 만들면 신장트리라고 한다.
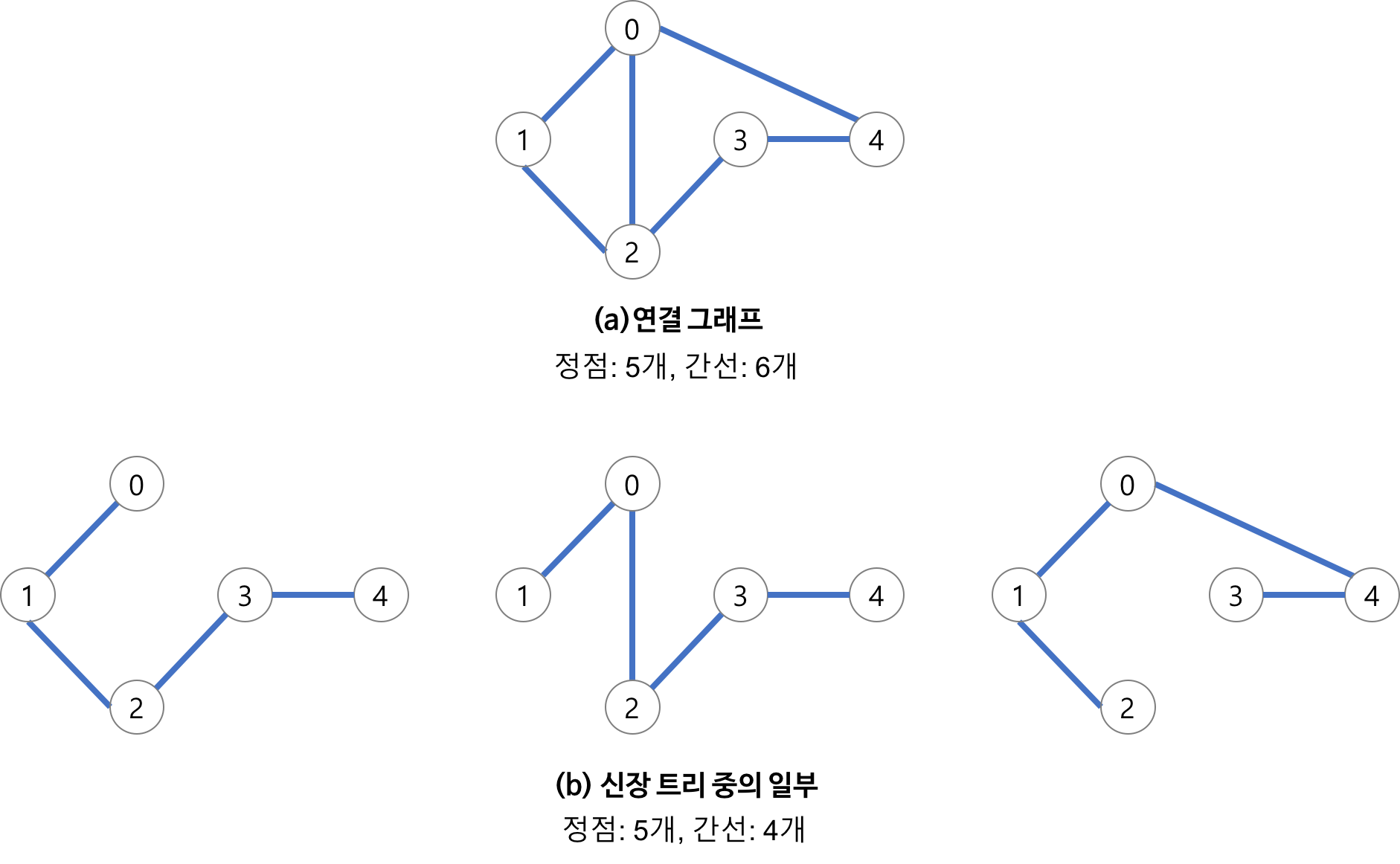
트리로 만들었기 때문에 간선의 수는 정점이N개 일때 정확히 N-1개가 된다.
트리일 경우 항상 간선은 N-1이 되는건 맞지만 위의 예시 처럼 반드시 직선이 되지는 않는다. 아래 MST예시 참조

최소신장트리는 신장트리중 간선 가중치합이 최소인 트리를 말한다.
간선가중치가 없을 때는 O(N-1)임이 명확하므로 Trivial 하다(이 문제 참조)
최소신장트리를 구하는데는 크루스칼알고리즘과 프림알고리즘이 있다.
둘다 음수가중치가 있어도 정상 동작가능하다.
크루스칼(Kruskal) 알고리즘(간선중심)
선행지식: 유니온 파인드(Union-Find)
간선중심이라 첫 간선이 최종답안에 포함되지 않을 수 있다.
> 근데 아닌듯. 소팅한다음에 최소 간선부터 시작인데 이건 무조건 포함하는듯하다.
가중치 오름차순으로 간선을 소팅한다음 union find로 사이클 체크하면서 사이클이 아닌경우 가중치합을 구해주면 된다.(무척간단)
중간과정에서는 정점별로 그룹이 생겨서 사이클도 판단하고 그렇지만, 유니온파인드 과정을 마치고 나면 모든 정점은 하나의 그룹에 포함되게 된다(이점 주의)
여기에 설명 잘되어 있고, 아래는 내 구현이다. 이 문제의 답안이기도 함
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
#include <bits/stdc++.h>
using namespace std;
struct node { int u, v, w; };
int MST_Kruskal(int max_v, vector<node>& v) {
struct union_find {
vector<int> parent;
union_find(int n) {
parent.resize(n + 1);
for (int i = 0; i <= n; i++) parent[i] = i;
}
int find(int x) {
int ox = x;
while (parent[x] != x) x = parent[x];
return parent[ox] = x;
}
void uni(int x, int y) {
int xp = find(x), yp = find(y);
parent[yp] = xp;
}
};
sort(v.begin(), v.end(), [](node& a, node& b) {return a.w < b.w; });
union_find uf(max_v);
int ans = 0;
for (auto a : v) {
if (uf.find(a.u) == uf.find(a.v)) continue;
uf.uni(a.u, a.v);
ans += a.w;
}
return ans;
}
int V, E, A, B, C;
int32_t main()
{
cin >> V >> E;
vector<node> v;
for(int i=0;i<E;i++) cin >> A >> B >> C, v.push_back({ A,B,C });
cout << MST_Kruskal(V, v) << endl;
return 0;
}
|
cs |
간결한 풀이를 위해 일반적인 인접리스트와 다르게 {u, v, w}자체를 백터로 전달했음에 주의(union-find특징상 이렇게 간단히 전달해도 잘 풀림)
위 코드의 경우 모든 정점이 사용되지 않아도 정상MST로 판정하는데 해당 부분을 수정한 코드는 아래와 같다.(base1도 추가)
struct node { int u, v, w; };
int MST_Kruskal(int max_v, vector<node>& v, bool base1=false) {
if (base1) max_v++;
struct union_find {
vector<int> parent;
int components;
union_find(int n) : components(n) {
parent.resize(n + 1);
for (int i = 0; i <= n; i++) parent[i] = i;
}
int find(int x) {
int ox = x;
while (parent[x] != x) x = parent[x];
return parent[ox] = x;
}
void uni(int x, int y) {
int xp = find(x), yp = find(y);
if (xp != yp) {
parent[yp] = xp;
components--;
}
}
};
sort(v.begin(), v.end(), [](node& a, node& b) {return a.w < b.w; });
union_find uf(max_v);
int ans = 0;
for (auto a : v) {
if (uf.find(a.u) == uf.find(a.v)) continue;
uf.uni(a.u, a.v);
ans += a.w;
}
if (uf.components != 1+base1) return -1; // 모든 정점을 사용하지 않으면 -1리턴
return ans;
}
크루스칼에는 소팅이 들어가기 때문에 보통 $O(E \times log(E))$로 계산하지만, 카운팅 소트가 가능한 경우는 $O(E)$로 계산되기도 하고,
전체가 다 소팅이 필요하다기 보다는 V-1개의 간선이 완성될때 까지만 필요하기 때문에, 힙소팅이 유리할수도 있는 측면이 있다.
관련하여 이런 논문도 발견
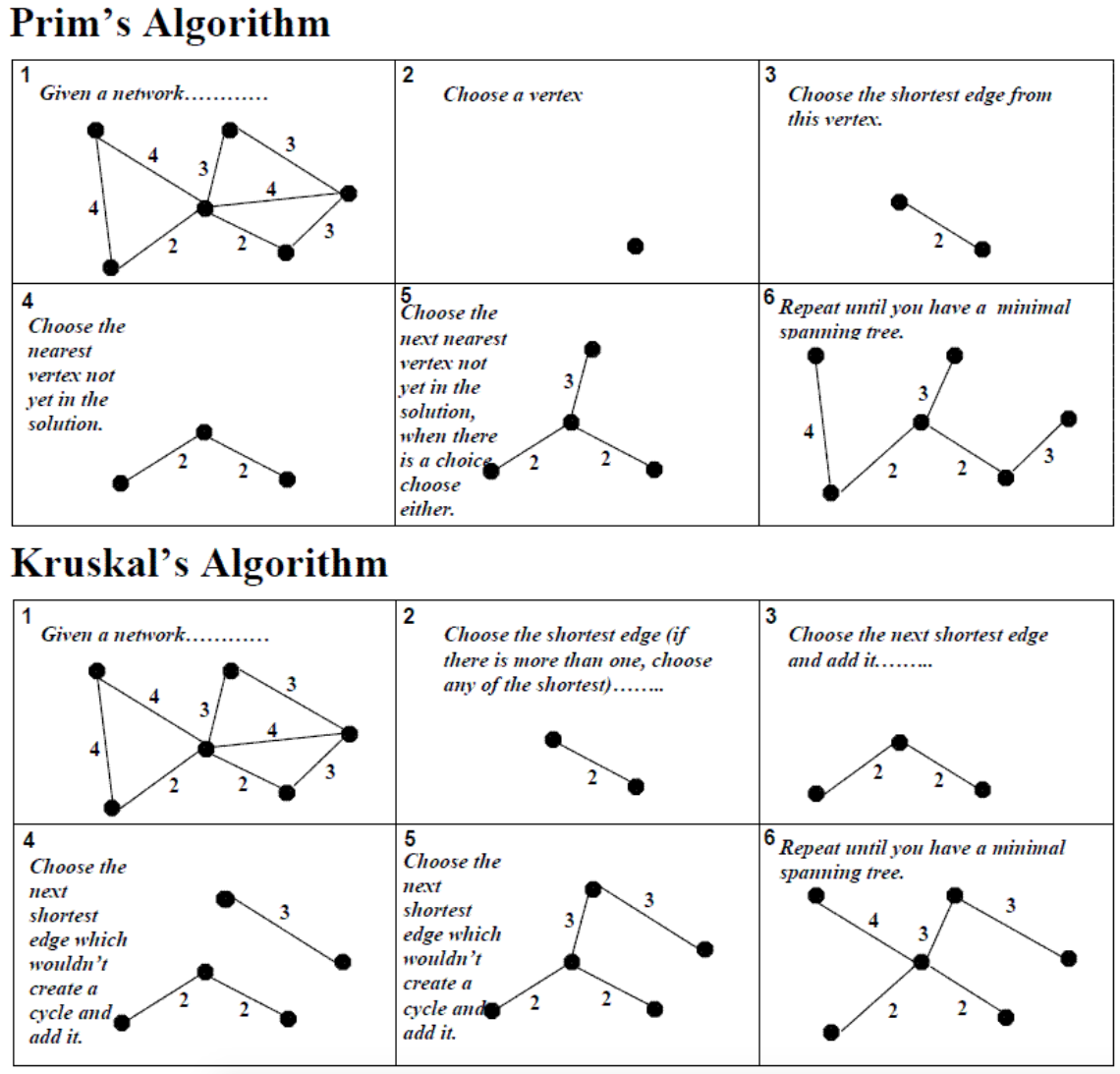
프림(Prim) 알고리즘(정점 중심)
선행지식: 너비 우선 탐색(Breadth-first search, BFS), 다익스트라 알고리즘 Dijkstra (필수는 아님)
정점 중심이라 시작정점은 MST에 꼭 포함되게 된다.(모든 정점이 포함되므로)
프림은 여기보면 예제 보면 설명 잘되어 있고, 설명을 보면 Queue를 쓴다고 되어 있고 우선순위큐 이야기가 나오기 때문에, 다익스트라 변형으로 풀 수 있을 것 같은 느낌이 든다. 그런데 아래 예제를 보면..
다익스트라는 1번에서 거리상 유리한 2번을 방문한다음에 1번에서 2번째로 집어넣은 3번을 방문하게 된다. 즉 간선으로 보자면 [1,2]간선을 방문하고 [1,3]간선을 방문하게 되는데, 프림알고리즘 상에서는 [1,2]간선을 방문한다음 [2,3]간선과 [1,3]간선을 비교해서 [2,3]간선이 더 비용이 싸므로 먼저 방문하게 된다는 점에서 다익스트라와 차이점을 발견했다. 게다가 음수사이클이 있을때 다익스트라는 무한루프에 빠지게 되는데, 프림에서는 한번 방문한 노드를 다시 방문하지 않는 식으로 방문처리도 다르게 해야한다.
아래는 내가 수정해본 코드이고, 위의 크루스칼과 같은 문제의 답안이기도 하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
#include <bits/stdc++.h>
using namespace std;
struct node { int v, w; };
bool operator<(node l, node r) { return l.w > r.w; }
// 다익스트라와의 차이
int MST_Prim(int max_v, int start_v, vector<vector<node>>& adj_list) {
vector<int> visit(max_v + 1, 0);
priority_queue<node> q; q.push({ start_v, 0 });
int sum = 0; // 1. 글로벌썸 처리
while (q.size()) {
node n = q.top(); q.pop();
if (visit[n.v]) continue; // 2. min_dist대신 visit처리
visit[n.v] = 1;
sum += n.w;
for (auto adj : adj_list[n.v]) {
q.push({ adj.v, adj.w }); // 3. visit처리를 여기서 하면 안됨
}
}
return sum;
}
int V, E, A, B, C;
int32_t main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin >> V >> E;
vector<vector<node>> adj_list(V + 1);
for (int i = 0; i < E; i++)
cin >> A >> B >> C,
adj_list[A].push_back({ B,C }),
adj_list[B].push_back({ A,C });
cout << MST_Prim(V, 1, adj_list) << endl;
return 0;
}
|
cs |
크루스칼 vs 프림
일반적으로는 간선이 sparse 할수록 크루스칼이 유리하고 dense할수록 프림이 유리한걸로 알려져 있다.
크루스칼의 시간 복잡도는 정렬하는데 $O(E \times log(E))$정도 걸리고, 유니온파인드 하는데 $O(E)$정도 걸리므로, 전체적으로 $O(E \times log(E))$정도로 보면 될 것 같다.
프림의 복잡도는 다익스트라와 비슷하게 $O((V+E)\times log(V))$이다. (우선순위큐를 쓴 경우이며, 피보나치힙을 쓴경우는 좀 더 내려간다)
Dense한 그래프의 경우는 $E=V^2$정도이므로 크루스칼은 $O(V^2 log(V^2))$, 프림은 $O(V^2 log(V))$정도로 보면 될거 같다.
Sparse(V > E)한 그래프의 경우는 크루스칼은 $O(E \times log(E))$, 프림은 $O(V \times log(V))$가 되므로 크루스칼이 유리하다.
'Programming > Algorithm' 카테고리의 다른 글
| 트리DP (0) | 2020.04.15 |
|---|---|
| 세그멘트 트리 (0) | 2020.04.13 |
| 유니온 파인드(Union-Find), 서로소 집합(Disjoint Set) (0) | 2020.04.10 |
| 그래프 최장거리, 최대이득, 최다비용등 (1) | 2020.04.09 |
| 비트연산 (0) | 2020.04.02 |



