Sevity Blog

일반적으로 셔플 알고리즘을 떠올리면 다음과 같은 naive solution을 생각하기 쉽다.

void LnNumber::ShuffleArray(long* arr, long count)
{
      for (int i=0;i<count;i++)
      {
            long toInx = rand() % count;
            {//swap
                  long temp = arr[i];
                  arr[toInx] = arr[i];
                  arr[i] = temp;
            }
      }
}

하지만 위 코드는 순진해보이는 겉모습과 다르게 엄청난 바이어스를 포함하고 있는데,

카드 3장의 모든 순열은 3!(=3 x 2 x 1) = 6이지만 위의 toInx를 보면 3 x 3 x 3 = 27로 6으로 나눠떨어지지 않는 경우의 수를 가지고 있다!

따라서 아래처럼 덜 직관적이지만 n!에 맞춘 경우의 수를 가진 코드로 수정해줘야 한다.

이 코드를 Fisher-Yates shuffle이라고 한다.

void LnNumber::ShuffleArray(long* arr, long count) {
    for (int i = count - 1; i > 0; i--) {
        long toInx = rand() % (i + 1); // 0부터 i까지의 랜덤한 인덱스(i포함)
        // swap
        long temp = arr[i];
        arr[i] = arr[toInx];
        arr[toInx] = temp;
    }
}

이코드의 toInx를 보면 카드3장의 예시에서 3 x 2 x 1 = 6 = 3!의 경우의 수를 가진다.

sort

가장 기본적인 sort는 Array.sort()또는 Collections.sort()를 쓰면 된다. (char[] 같은건 전자만 가능한듯?)

struct node 같은걸 쓰면서 특정 필드에 대해 소팅하고 싶으면 다음 기법을 쓰자.

class Tweet {
    Long time;
    int tweetId;
}
List<Tweet> feed;
...

//time에 대해서 sort하고 싶을때
feed.sort((t1, t2) -> t1.time.compareTo(t2.time));  
//역순을 원하면 t1, t2를 바꿔준다.
feed.sort((t1, t2) -> t2.time.compareTo(t1.time));

//약간 올드하게 아래처럼도 가능
Collections.sort(feed, new Comparator<Tweet>() {
    @Override
    public int compare(Tweet t1, Tweet t2) {
        return t1.time.compareTo(t2.time);
    }
});

여러 필드에 대해서 복잡하게 정렬해야하면 아래 방법 사용

feed.sort(Comparator.comparing((Tweet t) -> t.time)
                   .thenComparing(Comparator.comparing((Tweet t) -> t.tweetId).reversed()));

LIS(Longest Increasing Subsequence)는 가장 긴 증가하는 부분 수열을 찾는 알고리즘이다.

즉, 주어진 수열에서 일부 숫자를 제거하여 만든 부분 수열 중에서, 오름차순으로 정렬된 가장 긴 수열을 찾는 문제.
예를 들어, 수열 [10, 20, 10, 30, 20, 40]이 있다면, LIS는 [10, 20, 30, 40]이 된다.

예시 백준 문제는 여기 있다.

DP를 연습할때 가장 먼저 나오는 문제이지만, 의외로 2가지 실수하기 쉬운 포인트와. 한가지 인사이트를 제공한다.

2가지 실수하기 쉬운 포인트

아래는 이문제에 대한 정답코드인데, 아래 주석으로 여기라고 되어 있는 부분을 풀때마다 실수했다.

#include <stdio.h>
#include <algorithm>
using namespace std;

// dp[3] = 5 ; 인덱스 3까지 가장 긴 증가하는 부분수열의 길이는 5이다.
int dp[1001]; 
int A[1001];

int main(void)
{
	int N; scanf("%d", &N);
	for (int i = 0; i < N; i++) scanf("%d", A + i),dp[i]=1;  // 여기. dp[i]=1초기화 부분!
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < i; j++) {
			if (A[i] > A[j]) 
				dp[i] = max(dp[i], dp[j] + 1);
		}
	}
	int ans = 1;
	for (int i = 0; i < N; i++) ans = max(ans, dp[i]);  // 여기. dp[n-1]아니어도 답이 될 수 있음!
	printf("%d\n", ans);
	return 0;
}

한가지 인사이트

이 문제는 놀랍게도 recursive+memoization보다 iterative 방식이 더 생각하기 편하고,

편한 recursive+memoization을 떠올리면 dp[ix][cur_val] 형태가 돼서 냅색DP형태가 나오는데 문제 범위에 따라 메모리초과 오류가 발생하여 해결이 어렵다.

아래는 편한 recursive버전이다.

#include <bits/stdc++.h>
using namespace std;
int dp[1001][1001];
int in[1001];
int n;
int dfs(int ix, int cur_max_val){
    if(ix>=n) return 0;
    if(dp[ix][cur_max_val]) return dp[ix][cur_max_val];
    
    //포함
    int r1 = -1;
    if(cur_max_val < in[ix])
        r1= 1 + dfs(ix+1, in[ix]);
    
    //불포함
    int r2 = dfs(ix+1, cur_max_val);

    return dp[ix][cur_max_val] = max(r1,r2);
}
int main() {
    scanf("%d", &n);
    for(int i=0;i<n;i++) scanf("%d", in+i);
    printf("%d\n", dfs(0, 0));

    return 0;
}

자세히 들여다 보면, dp[n]을 1로 초기화 하는 부분도 필요없고, 마지막에 정렬하는 부분도 필요없어서 실수 확률이 확연히 줄어든다.

하지만 위 코드를 dp[ix]로 1차원만 사용하도록 변경하는건 쉽지 않다.

아래처럼 할 수 있긴한데, dfs함수내에 iterative한 부분이 들어 있어 완전한 DFS라고 부를 수 있을지 약간 애매하다.

#include <bits/stdc++.h>
using namespace std;
#define FOR(i,a,b) for(int i=(a);i<(b);++i) 
#define REP(i,n) FOR(i,0,n) 
typedef vector<int> VI;

int dp[1001];
int in[1001];
int N;
int go(int n)
{
         if(n==0) return 1;
         if(dp[n]) return dp[n];
 
         int maxR=1;
         REP(i,n){
            if(in[n] >in[i])
                maxR = max(maxR, go(i)+1);                 
         }
         return dp[n] = maxR;
}
 
int main()
{
        scanf("%d\n", &N);
        REP(i, N)scanf("%d",&in[i]); 
        int r=0;
        REP(i,N) r=max(r,go(i));
        cout << r <<endl;
        return 0;
}

실제 시퀀스를 출력하는 방법

아래처럼 prev배열하나를 추가하면 어렵지 않게 구현가능하다.

#include <stdio.h>
#include <algorithm>
using namespace std;

// dp[3] = 5 ; 인덱스 3까지 가장 긴 증가하는 부분수열의 길이는 5이다.
int dp[1001];
int A[1001];
int prv[1001];

int main(void)
{
    fill(prv, prv + 1001, -1);
    int N;
    scanf("%d", &N);
    for (int i = 0; i < N; i++)scanf("%d", A + i), dp[i] = 1; // 여기. dp[i]=1초기화 부분!
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < i; j++)
        {
            if (A[i] > A[j])
                if (dp[j] + 1 > dp[i])
                {
                    dp[i] = dp[j] + 1;
                    prv[i] = j;
                }
        }
    }
    int ans = 1;
    int end_ix = 0;
    for (int i = 0; i < N; i++)
    {
        if (ans < dp[i])
        {
            ans = dp[i];
            end_ix = i;
        }
    }
    printf("%d\n", ans);
    vector<int> v;
    v.push_back(A[end_ix]);
    while (prv[end_ix] != -1)
    {
        end_ix = prv[end_ix];
        v.push_back(A[end_ix]);
    }
    reverse(v.begin(), v.end());
    for (auto e : v)
        printf("%d ", e);

    return 0;
}

여기를 참조했다.

아래 코드에서 find_intersection 함수를 라이브러리로 활용하자.

이 문제의 정답이기도 하다.

#include <bits/stdc++.h>
#define int long long
using namespace std;
#define REP(i,n) for(int i=1;i<=(int)(n);i++)

struct point { double x, y; 
    bool operator==(const point& other) const {return x == other.x && y == other.y;}
    bool operator<=(const point& other) const {return y < other.y || (y == other.y && x <= other.x);}
    bool operator>(const point& other) const {return y > other.y || (y == other.y && x > other.x);}
};
double CCW(point A, point B, point C, bool sign_only=true) {
    double r = (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);
    if (sign_only == false) return r;
    if (r == 0)return 0;
    return r > 0 ? 1 : -1;
}
struct line { point s, e; };
//touch_ok가 false이면, 두 선분이 교차하지 않고 만나기만 하는 경우에는 false를 리턴
bool Intersect(line x, line y, bool touch_ok=false) {
    point a = x.s, b = x.e;
    point c = y.s, d = y.e;
    double ab = CCW(a, b, c) * CCW(a, b, d);
    double cd = CCW(c, d, a) * CCW(c, d, b);
    if (ab == 0 && cd == 0) { // 이건 두 선분이 평행한 경우
        pair<double, double> aa = { a.x, a.y }, bb = { b.x,b.y }, 
            cc = { c.x, c.y }, dd = { d.x,d.y };
        if (aa > bb)swap(aa, bb);
        if (cc > dd)swap(cc, dd);
        if(touch_ok) return cc <= bb && aa <= dd; // 0이면 점끼리 만나는 것
        return cc < bb && aa < dd; // a<d이면서 b,c가 교차하면 선분
    }
    if(touch_ok) return ab <= 0 && cd <= 0; // 0이면 두 선분이 한점에서 만나는 것
    return ab < 0 && cd < 0; // 이게 기본. 각선분에서 나머지 2개점 방향이 달라야 교차
}

bool find_intersection(line l1, line l2, point& out) // 교점 구하기
{
    point A = l1.s, B=l1.e, C=l2.s, D=l2.e;
	if (A > B) swap(A, B);
	if (C > D) swap(C, D);
	double px = (A.x * B.y - A.y * B.x) * (C.x - D.x) - (A.x - B.x) * (C.x * D.y - C.y * D.x);
	double py = (A.x * B.y - A.y * B.x) * (C.y - D.y) - (A.y - B.y) * (C.x * D.y - C.y * D.x);
	double p = (A.x - B.x) * (C.y - D.y) - (A.y - B.y) * (C.x - D.x);

    bool found = false;
	if (p == 0) // 평행할 때
	{
		// 교점이 하나일 때
		if (B == C && A <= C) found=true, out = B;
		else if (A == D && C <= A) found=true, out = A;
	}
	else // 교차할 때
	{
		double x = px / p;
		double y = py / p;
        out = {x,y};
        found=true;
	}
    return found;
}


int32_t main()
{
    ios::sync_with_stdio(0); cin.tie(0);
    vector<line> l;
    double a, b, c, d; REP(i, 2)cin >> a >> b >> c >> d, l.push_back({ a,b,c,d });
    if(Intersect(l[0], l[1], true)==false) puts("0");
    else{
        puts("1");
        point intercection;
        bool found = find_intersection(l[0], l[1], intercection);
        if(found) printf("%.16lf %.16lf", intercection.x, intercection.y);
    }
    return 0;
}

여기, 여기 참조

브루트포스로 풀기에는 N이 약간만 너무 클때, 

분할정복처럼 절반씩 나누고 연산한다음 합치는 연산을 하는걸 meet in the middle이라고 한다.

분할정복처럼 반복적으로 나누고 합치고 하지는 않고 1회성으로만 하는거 같다.

합치는 연산은 문제마다 다르며, 투포인터가 사용될때도 있다.

샘플 문제는 여기를 참고하자.

아직 정확히 모르는점들

meet in the middle을 반복하면 계속해서 복잡도를 줄일 수 있는가? 만약 가능하다면 분할정복과의 차이점은?

합치는 연산에서 투포인터 말고 다른게 쓰는 예는 어떤게 있는가?

• 요건 이분탐색이 있는데, 이분탐색도 직접구현 기준으로 보면 left, right 포인터를 쓰는거라 투포인터의 일종으로 볼 수는 있을듯?

투 포인터는 한 가지 알고리즘을 말하는 것이라기보다,

포인터 i, j 두 개를 사용해서, 브루트 포스로는 O(N^2)이 걸리는 문제를,

O(N)으로 만드는 그리디 알고리즘의 모음라고 보는 게 좋다.

따라서, 투 포인터는 예제를 통해서 익히는 게 좋고,

투 포인터를 통해서 그리디가 가능한 문제는 부분합,

배열의 두 값의 합이나 차가 특정 수가 되는지(A [i]+A [j]=S) 찾는 문제 등이 있다.

위 링크들은 백준 문제로 연결된다.

구현 난이도는, 아무래도 그리디다 보니 조건절이 브루트 포스보다는 더 들어가야 해서,

조금 더 어렵고 주의를 요한다고 볼 수 있다.

위처럼,

어떤 그래프를 V1과 V2 그룹으로 나누었을때,

그룹내의 정점끼리는 간선이 없고 그룹간 간선만 존재할 때 이분 그래프라고 한다.

주어진 그래프가 이분 그래프인지 판정하기

undirected 이면서 모든 두 꼭지점의 연결 경로가 존재하는 연결 그래프(connected graph)인 경우,

아무노드나 잡고, BFS나 DFS로 위처럼 색칠을 해 나가다가 색깔의 conflict 가 있으면 이분 그래프가 아니고, 없으면 이분 그래프로 판정 가능하다.

undirected 이면서 연결 그래프는 아닌경우(위의 그림1도 연결그래프는 아님),

이경우도 단순하게 분리된 각각의 연결 그래프에 대해서 모두 위의 색칠로직을 적용해주면 됨(모든 분리된 그래프가 이분 그래프여야 전체도 이분그래프인걸로 판정)

아래 소스코드 참조. 이 문제의 답안이기도 하다.

directed인경우,

이 경우도 판정 가능한거 같은데, 자세히 알아보진 않았다.

여기, 여기, 여기, 여기 참조

특히 여기가 좋다.

완전이진트리 형태의 자료구조를 이용해서, element update가 존재하는 배열에 대해 특정 구간의 합, 곱, 최대값, 최소값 등을 효율적으로 구하는 자료구조

힙(heap)도 완전 이진트리를 이용하기 때문에 유사성이 있다고 볼 수 있다.

중간 중간에 element update가 존재하지 않는 경우, 세그먼트 트리까지는 필요없고 prefix sum등 간단한 테크닉을 쓰면 된다.

arr[12] = {3, 5, 6, 7, 2, 9, 4, 5, 2, 8, 1, 5} 이러한 배열이 있다고 하자.

완전이진트리 형태로 만들것이므로 $2^k >= 12$인 최소 k를 구해야한다. 

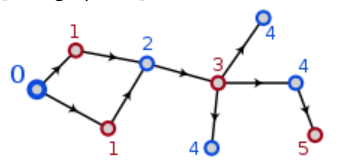
여기, 여기, 여기, 여기 참조

수학적인 기초

먼저 절, 명제, 조건문 이 세가지가 헷갈리기 쉬운데, 이 알고리즘을 이해하려면 절대 헷갈리면 안된다.

절은 나중에 설명하고 명제부터 살펴보자.

명제란 대한민국의 수도는 서울이다, 사람은 날 수 있다. 처럼 true/false를 특정지을 수 있는 것을 말한다. 

나는 사람이다. 라는 명제를 P로 놓고, 나는 동물이다. 라는 명제를 Q로 놓은 다음 화살표로 연결하면

P->Q 이렇게 되고 조건문이된다.

조건문의 true/false는 생각보다 까다로운데 명제논리 링크를 참조해서 이해해보자.

위에서 다른건 다 상식선에서 이해가 되는데 P가 거짓이면 Q가 참이던 거짓이던 모순이 없는건 일상생활 명제에 대입하면 좀 받아들이기 힘들다.

(철희가 남자라면 철희는 남자가 아니다. 라는 조건문도 모순이 없는 참이 되어버리는 사태가 발생한다. 근데 생각해보면 남자라면 이라는게 거짓일때만 모순이 없는것이므로, 남자라는게 뻥이었으므로 뻥이 아닌 사실로는 남자일수도 있고 아닐수도 있는 상태가 되는걸로 이해는 가능하다. )

그럴때는 다음 문장을 참고해서 대략적으로 이해하고 넘어가자

P가 거짓일 때 참이되는 것이 아직 받아들이기 어렵다면 이렇게 생각해보자. 선생님이 학생에게 '체육대회에서 100m를 5초안에 뛸 수 있으면 72 km/h... 아이스크림을 주겠다'라고 말했다고 해보자. 이 말이 거짓말이 되는 경우는 "단 한가지" 뿐이다. 즉, (2) 학생이 100m를 5초 안에 들어왔는데 선생님이 아이스크림 안주는 경우만 거짓이다. (3) 학생이 5초안에 못뛰었을 때 선생님이 학생이 안쓰러워 아이스크림을 사준 경우 이는 선생님이 약속을 어겼다고 볼 수 없고 단순한 변심으로 보는게 타당할 것이다. 즉 위의 선생님의 약속(가언 명제) 자체는 여전히 참이다. 그리고 마찬가지로 (4) 5초안에 못뛰었을 때 선생님이 아이스크림을 사주지 않는 경우 학생은 그런가보다 하고 넘어갈 수 있고 이 또한 선생님이 약속(가언 명제)을 어겼다고 할 수 없다. 즉, 참으로 인정한다. 다시 정리하자면 학생이 100m를 5초 안에 뛰지 못한 경우에 대해서 선생님은 어떠한 약속도 하지않았으므로 선생님이 어떤 행동을 하든 약속이 거짓말이 될 수없다.[12]

2SAT이란

2-SAT(2-SATisfiability)문제는 충족 가능성 문제(satisfiability problem)의 한 종류입니다.

충족 가능성 문제란, 여러 개의 boolean변수들로 이루어진 식이 있을 때 각 변수에 값을 할당하여 식을 참으로 만드는 조합을 찾거나, 그러한 조합이 없음을 찾는 문제입니다.

f = (x2 ∨ ￢x1) ∧ (￢x1 ∨ ￢x2) ∧ (x1 ∨ x3) ∧ (￢x2 ∨ ￢x3) ∧ (x1 ∨ x4)

이 식은 {x1 : false, x2 : false, x3 : true, x4 : true} 인 경우에 참이 됩니다.

가만 보면, 나이브한 솔루션은  x1~x4값에 대해서 0과1을 대입해보는 식으로 2^n의 모든 부분집합을 테스트해보면 된다는 사실을 알 수 있다. 

위에보면 괄호안에 두개의 변수가 들어있는데, 그래서 2-SAT이고, 괄호하나를 절(clause)이라고 부른다.

괄호안은 항상 OR 연산자, 괄호밖은 항상 AND연산자로 되어 있다. 

이렇게 절의 AND 연산으로만 표현된 식의 형태를 CNF(Conjunctive Normal Form)라고 합니다.

1SAT문제는 트리비얼하게 O(N)에 풀린다.

3SAT이상은 다항시간 솔루션이 없다.

신기하게도 2SAT문제도 선형시간에 풀린다!

여기까지만 들으면 이런걸 왜 보고 있나하는 생각이 드는데, 의외로 많은 문제들이 2-SAT으로 변환 가능하고, SCC로 풀수 있다고 한다.

여기 참조

1. 답이 존재하는지 여부 구하기

여기까지는 할만한 느낌

핵심아이디어

1. 논리식을 조건문으로 바꾼다 : (A∨B) = ¬A → B 와 ¬B → A  !!

A가 거짓이라면 B는 무조건 참이여야 하며, B가 거짓이라면 A는 무조건 참이여야 한다.

2. 모든 절의 명제들을 합하여 하나의 유향그래프를 생성할 수 있다.

3. 사이클 전체가 true이거나 전체가 false로 통일되어야한다. A와 ¬A이 같은 사이클에 있을 수 없다.

3번을 잘 이해해야 하는데, true -> false이면(사실 그럴때만) 조건문에 모순이 생긴다는 걸 기억하면 된다.

(p → q에서 p가 참일 때는 q는 무조건 참이여야하며 p가 거짓일 때는 q가 무엇이든지 상관없음)

따라서, A→¬A가 나오면 A는 반드시 false여야 한다.

마찬가지로 ¬A→A가 나오면 A는 반드시 true여야 함

근데 (하나의 사이클에서 ) A→¬A도 발견되고 ¬A→A도 발견된다? 그럼 false도 될수 없고, true도 될수 없어서 모순!

(여기서 한가지 중요한 관찰은 같은 SCC가 아니면서 A→¬A 또는 ¬A→A 이렇게 단방향은 있을 수 있다는 것이다. 일상언어 조건문으로 바꾸면 남자이면 남자가 아니다. 이런게 되어서 무지 이상하지만, 상단에 서술했듯이 수학적으로는 모순이 없다. 조건문 왼쪽에 거짓이기만 한다면.)

내 코드는 다음과 같다. 이 문제의 답안이기도 하다.

2. 유효한 변수값들 구하기

난이도가 확 올라가는 느낌

여기, 여기 참조

추가로 필요한 아이디어

모든 정점에 대해서 위상정렬 순으로 처음만나면 거짓을 만들어주는식으로 채워주면 된다.

예를 들어 위상정렬순으로 not X3을 먼저 만났으면 not X3 = false 가 되어야 하므로 X3은 true로 확정해주는 식.

이런방법 말고도 굉장히 많은 방법이 있는것 같은데, 적당히 한가지로 외워두면 될듯하다.

아래는 내 코드고, 이 문제에 대한 답안이기도 하다.

여기, 여기 참조, 강한연결요소(SCC)의 타잔 알고리즘과 관련있다.

단절점

한덩이의 무방향 그래프에서 한 정점을 제거했을 때 그래프가 두개 이상으로 나누어지면 단절점이라고 한다.

단절점을 가장 Naive하게 찾아 볼 수 있는 방법은 모든 정점을 한번씩 선택하여(V) 제거한 후 그래프가 나뉘어지는지 파악해보는 방법이 있다(V + E). 따라서 시간 복잡도는 $O(V \times (V + E))$가 된다.

보통 나이브 하지 않은 구현은 O(V+E)의 복잡도를 가지는데, 여기가 가장 이해하는데 도움이 됐다.

그 알고리즘을 살펴보면, 각 정점에 대해서 DFS트리를 만들면서, 다음 두가지를 기록한다.

1. 해당 정점을 방문한 순서: 이를 ord이라고 하자.

2. 해당 정점을 루트로 하는 서브트리로 부터 연결된 정점중 가장 작은 ord 값: 이를 low라고 하자.

그다음 해당 정점을 리턴하기전에 ord와 low를 비교해서 low가 ord보다 작으면 우회경로가 존재하므로 단절점이 아닌것으로 판단.

예를 들어 아래와 같은 그래프가 있을때

먼저 DFS트리를 그려보면 다음과 같다.(트리는 방향그래프가 아니나 이해를 위해 방향그래프로 표했다. 역방향 화살표가 하나있는데 이는 물론 트리의 구성요소는 아니고 back edge이다.)

괄호안의 숫자두개는 (ord, low)가 된다.

edge(u, v)가 아래방향 화살표인 tree edge라면, low[u] = min(low[u], low[v])가 되고,

edge(u, v)가 위쪽방향 화살표인 back edge라면, low[u] = min(low[u], ord[v])가 된다.

(이규칙에 맞는지 위의 그림을 잘 살펴보자)

말단노드가 아니면서 ord <= low 이면 단절점이므로 위 그래프에서는 단절점은 1, 6, 7이다.

(루트의 경우는 자식 노드가 2개 이상인지로 별도 판단)

근데, 실제로는 ord[n], low[n]을 다 구한다음에 후처리로 단절점을 판단하면 아래와 같은 반례때문에 잘되지 않았다(4번 노드가 문제인데 low[4]값은 최종적으로 1이 된다. 그러므로 후발적으로 ord <= low를 판단하면 단절점이 아닌것으로 판단된다)

그래서 low[n]을 최종판단하기전에 중간과정에서 자식노드중 하나라도 ord <= 자식트리의 low 인 순간에 즉발적으로 단절점을 판단해줘야했다. 자세한 사항은 아래 코드를 참조하자.이 문제의 답안이기도 하다.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56

#include <bits/stdc++.h> using namespace std; #define REP(i,n) for(int i=0;i<n;i++) #define REP1(i,n) for(int i=1;i<=n;i++) using vi = vector<int>; using vvi = vector<vi>;   int32_t main() {     ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);     int V,E;cin>>V>>E;     vvi adj_list(V + 1);     REP(i, E)     {         int A,B;cin>>A>>B;         adj_list[A].push_back(B);         adj_list[B].push_back(A);     }     set<int> ans;     //아래에서 visit는 ord와 통합가능하지만, 가독성을 위해 남겨둠     vi visit(V + 1), ord(V + 1), parent(V + 1), root(V + 1); int g_ix = 0;     function<int(int, int)> dfs = [&](int n, int par)-> int  // low를 리턴     {         visit[n] = 1;         ord[n] = ++g_ix;         int low = ord[n];         int child = 0;         for (auto adj : adj_list[n])         {             if (adj == par) continue;             if (visit[adj])  // 백엣지의 경우                 low = min(low, ord[adj]);  // 접근가능한 back정점의 순서로 업데이트             else {  // 트리엣지의 경우                 child++;                 int r = dfs(adj, n);                   // 루트가 아니고 자식트리중 하나라도 자신위로 올라가지 못하면                 if(par!=-1 && r>=ord[n])                   {                     // 전체 자식노드를 보는게 아니라 즉발기로 동작함에 유의                     // 주의할점은 현재 정점의 low값을 최종결정하기전에                     // 단절점 판정이 이루어지는 부분                     ans.insert(n);                 }                 low = min(low, r);             }         }         // 루트이고 자식이 2개이상이면         if (par == -1 && child > 1) ans.insert(n);         return low;     };     REP1(i, V)if (visit[i] == 0)dfs(i, -1), root[i] = 1;     cout << (int)ans.size() << endl;      for (auto a : ans) cout << a << ' ';     cout << endl;     return 0; } Colored by Color Scripter

cs

단절선

단절점 소스코드와 개념을 거의 그대로 활용할 수 있고, 아래 두가지 부분만 다르다.

1. 루트노드란 개념이 사라진다.

2. r >= ord[n] 조건이 r>ord[n] 으로 등호가 하나 사라진다.

2번에 대해서는 예제 입력인 아래 그래프에서  1번(루트) 정점을 기준으로 생각하면 등호인경우 사이클이 생겨서 단절선이 아님을 확인할 수 있다.(아래 그림 참조)

여기를 보면 해당 고민을 나보다 깊게 한 다른 블로그 포스팅을 볼 수 있다.

소스코드는 아래와 같고, 이 문제의 답안이기도 하다.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53

#include <bits/stdc++.h> using namespace std; #define REP(i,n) for(int i=0;i<n;i++) #define REP1(i,n) for(int i=1;i<=n;i++) using vi = vector<int>; using vvi = vector<vi>;   int32_t main() {     ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);     int V, E; cin >> V >> E;     vvi adj_list(V + 1);     REP(i, E)     {         int A, B; cin >> A >> B;         adj_list[A].push_back(B);         adj_list[B].push_back(A);     }     set<pair<int, int>> ans;     //아래에서 visit는 ord와 통합가능하지만, 가독성을 위해 남겨둠     vi visit(V + 1), ord(V + 1), parent(V + 1), root(V + 1); int g_ix = 0;     function<int(int, int)> dfs = [&](int n, int par)-> int  // low를 리턴     {         visit[n] = 1;         ord[n] = ++g_ix;         int low = ord[n];         for (auto adj : adj_list[n])         {             if (adj == par) continue;             if (visit[adj])  // 백엣지의 경우                 low = min(low, ord[adj]);  // 접근가능한 백정점 순서로 업데이트             else {  // 트리엣지의 경우                 int r = dfs(adj, n);                 // 자식트리중 하나라도 자신위로 올라가지 못하면                 if (r > ord[n])  // 단절점 케이스와 다르게 r == ord[n]인 경우 그려보면 사이클로 인해 단절선이 아님을 알 수 있다.                 {                     // 전체 자식노드를 보는게 아니라 즉발기로 동작함에 유의                     // 주의할점은 현재 정점의 low값을 최종결정하기전에                     // 단절점 판정이 이루어지는 부분                     ans.insert({ min(n,adj), max(n,adj) });  // 문제 조건에 따라 순서 조정                 }                 low = min(low, r);             }         }         // 단절선에서 루트정점이란 개념은 빠진다.         // if (par == -1 && child > 1) ans.insert(n);         return low;     };     REP1(i, V)if (visit[i] == 0)dfs(i, -1), root[i] = 1;     cout << (int)ans.size() << '\n';     for (auto a : ans) cout << a.first << ' ' << a.second << '\n';     return 0; } Colored by Color Scripter

cs

개념

SCC는 방향그래프 내에서 서브사이클을 이루는 집단들을 의미한다. 따라서 개념적으로는 강한연결요소라는 용어보다 강한연결집합이라는 용어가 더 적절해보이긴한다.

자세한 설명은 여기, 여기, 여기를 참조하면 개념에 대해서 어렵지 않게 파악 가능하다.

동작하는 원리에 대해 궁금하면 여기에 설명이 잘 나와있다.

활용도와 의의에 대해서는 여기에 잘 나와있다.

SCC를 구하는 알고리즘에는 크게 코사라주와 타잔이 있다.

코사라주(Kosaraju) 알고리즘

코사라주는 DFS두번 돌리면서 구하는 방법이고 여기, 여기를 보면 설명이 잘 돼있어서 쉽게 이해 가능하다. 

구현도 그냥 이해한 대로 술술 하면 되는 수준이었다.

왜 그런지 증명은 정확히 모르겠고 HOW는 파악이 어렵지 않다.

아래는 내가 직접 구현해본 코드이고, 이 문제의 답안이기도 하다.

dfs함수에서 마지막에 스택push하는 걸 보면 위상정렬개념이 들어간다는 사실을 알 수 있다.

타잔(Tarjan) 알고리즘

타잔 알고리즘은 생각보다 이해하기가 빡시다. 한가지 알아둘 것은 타잔 알고리즘이 SCC구할때 쓰는 알고리즘만 칭하는게 아니라, 여기서 쓰는 테크닉과 비슷하면 타잔이라고 부르는 것 같다는 점이다(타잔류?). 이건 확인은 필요

타잔의 경우, 결과값으로 SCC위상정렬까지 얻을 수 있어서, 이후 활용도에서 더 편하다.

타잔 알고리즘을 이해하려면, 먼저 트리 간선(tree edge), 순방향 간선(forward edge),역방향 간선(backward edge),교차 간선(cross edge)등 그래프 간선의 종류를 이해해야 한다.

그다음 단절선에 대한 이해를 해야한다. 그다음 여기 설명을 보면 이해하고 구현하기 좋다.

SCC타잔 알고리즘이 단절선 로직과 다른점은 다음과 같다.

1. 단절선 로직은 자식트리중 하나라도 현재간선보다 위로 못올라가면 바로, 단절선으로 판정하지만 SCC타잔에서는 전체 자식트리를 다 보고나서, 모든  자식트리가 현재간선보다 위로 못올라가면 SCC로 판정한다.

2. 단절선 로직과 다르게 스택을 운용하며, 처음 진입시 스택에 넣고 위의 1번 SCC판정조건이 만족되면 현재 정점까지 팝한다.

3. 단절선 로직은 visit배열만 사용하는데 반해서, SCC타잔은 finish배열도 추가적으로 사용한다. (물론 두 알고리즘 모두  visit배열대신 ord로 대체는 가능)

4. 단절선 로직은 tree-edge, back-edge만 고려하는데 반해서 SCC타잔은 추가적으로 cross-edge도 고려한다. (forward-edge는 둘다 무시)

단절선 코드를 변경해서 내가 구현해본 코드는 다음과 같다. 위와 같은 문제에 대한 답이기도 하다.