여기, 여기 좋다.
이 자료가 좋다고 하는데 아직 안 읽어 봄
information(정보량)
사건에 대한 확률이 드물수록 정보량은 크다
$1 \over p(x)$
두 사건이 동시에 발생할 확률은 곱해준다.
${1 \over p(x)} \times {1 \over p(y)}$
로그를 씌우면 언더플로도 막고 곱셈을 덧셈으로 바꿀 수 있다.
최종정보량 information = $\log{1 \over p(x)} + \log{1 \over p(y)} = - \sum \log p(i)$
시사점
정보량은 확률의 역수이고, 계산 편의성을 위해 log를 취했다.
log를 취한 것은 계산 편의성을 위한 것도 있지만, 필요한 비트수를 계산한다는 의미 부여를 할 수도 있다($\log_2$를 쓴 경우)
예를 들어 로그를 씌우기전 정보량이 40억으로 나왔는데 여기에 $\log_2$를 씌우면 31.x가 나올것이다.
이러면 이것의 의미를 이 정보를 전달하는데 필요한 비트수는 32비트이다. 이렇게 해석 하는 것..
entropy(정보량의 기댓값)
기대값 계산 공식 $E[X] = \sum_x xp(x)$
$E[f(X)] = \sum_x f(x)p(x)$
$E[-\log p(x)] = - \sum_x {{\log p(x)}p(x)}$
위 식에서 눈여겨 볼 부분은 p(x)가 두 번 쓰였는데.. 기대값 계산식을 들여다 보면 사건에 $-\log p(x)$가 쓰이고 확률분포에 $p(x)$가 쓰임
시사점
기대값은 일반적인 의미로 평균이라는 의미로 해석할 수 있고,
기대값을 구함으로써 개별 정보량에 비해서 평균적인 정보량(을 전송하는데 필요한 비트..로그이므로)이라는 관점으로 해석이 바뀐다.
예를 들어 위에서는 특정 정보를 전달하는데 필요한 비트수를 논했다면 여기서는 평균적으로 몇 비트가 필요하냐는 얘기로 바꿀 수 있다.
KL-divergence
두 확률간 상대적인 entropy를 뜻하며, cost function이 될 수 있다.
Q(x) 는 예측, P(x) 는 실제 확률이라고 하면, 이 값은 아래처럼 계산된다.
KL-divergence = 상대적인 엔트로피 = $E[-\log Q(x)] - E[-\log P(x)] $
(이때 확률 분포는 두 기대값 항 모두 P(x)를 사용)

 $=E[-\log Q(x)] - E[-\log P(x)] $
$=E[-\log Q(x)] - E[-\log P(x)] $
시사점
위에 식을 살펴보면 KL-divergence 식에서 확률분포는 P(x)로 고정한 상태에서 entropy의 차이를 구한다는 부분을 주목할 필요가 있다.
사실 왜 확률분포를 P(x)로 고정했느냐고 물어보면 이 건 아직 잘 모르겠다. KL-divergence의 정의와 관련된 부분이어서.. 원작자의 생각에 대한 공부가 좀 더 필요할듯
cross entropy
위의 KL-divergence로 cost function을 설계해보자
근데 이때 실제 확률인 P(x)는 상수취급하면
$E[-\log Q(x)] = -\sum \log q(x) p(x)$ 이 텀을 최소화 하는 문제로 변환된다.
 그리고 이렇게 H(p, q)로 표현한다.
그리고 이렇게 H(p, q)로 표현한다.
원래의 entropy 정의대로 하자면
$E[-\log Q(x)] = -\sum {{\log Q(x)}Q(x)}$ 이렇게 전개되는데..
예측 확률분포인 Q(x)대신 실제확률분포인 P(x)를 쓰면
$E[-\log Q(x)] = -\sum {{\log Q(x)}P(x)}$ 이렇게 되고 entropy가 아닌 cross entropy가 되는 것
P(x)와 Q(x)가 동일하면 cross entropy = entropy가 되면서 최소값이 되고.. 서로 많이 다르면 그 값이 커지는 구조다.
KL-divergence의 정의상 내부에 cross-entropy텀이 들어감을 눈여겨 보자.
조금 헷갈릴 수 있는 부분은 p와 q 어떤걸 고정하냐 이런 부분인데..이건 그냥 넘어가자 ㅋ
(이 부분이 헷갈릴 수 있다는 것은 위키설명에도 나와있다.)
중요한건 P(x)와 Q(x) 두가지 확률분포가 있을 때, 이 둘간의 차이를 cross entropy 텀으로 구할 수 있고 이게 손실함수가 될 수 있다는 것이다.
P(x)나 Q(x)모두 더해서 1이 되어야 하는 확률분포가 되어야 쓸 수 있기 때문에..
실제 분포인 P(x)의 경우 one-hot encoding을 해서 합이 1을 맞춰주고,
예측 분포이자 네트웍의 아웃풋이 되는 Q(x)의 경우 softmax를 통해 합을 1로 맞춰준다는걸 이해하는게 중요하다.
예제
예제는 여기에 잘나와있는거 같아서 따로 안적음
log-likelihood와의 연관성
만약 확률 변수 X가 $ {\displaystyle X=(X_{1},X_{2},\cdots ,X_{n})}$의 꼴로 주어져 있으며, $X_{i}$이 확률 분포로 ${\displaystyle P_{i,\theta }(X_{i})}$를 가진다면 가능도 함수와 로그 가능도 함수는 다음과 같다.
 $=-H(P, Q)$
$=-H(P, Q)$위 식을 보자.. 가능도(=likelihood)는 결국 모든 독립시행 샘플을 곱한걸로 구할 수 있는데, 여기에 로그를 씌운 로그-가능도의 경우 corss entropy의 음수값과 같아짐을 볼 수 있다.
그래서 cross entropy를 최소화 하는 문제는 결국 log-likelihood를 최대화 하는 문제와 같아지게 된다.
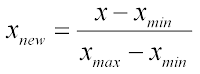
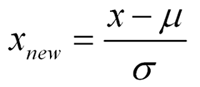


 $=E[-\log Q(x)] - E[-\log P(x)] $
$=E[-\log Q(x)] - E[-\log P(x)] $ 그리고 이렇게 H(p, q)로 표현한다.
그리고 이렇게 H(p, q)로 표현한다.
 $=-H(P, Q)$
$=-H(P, Q)$