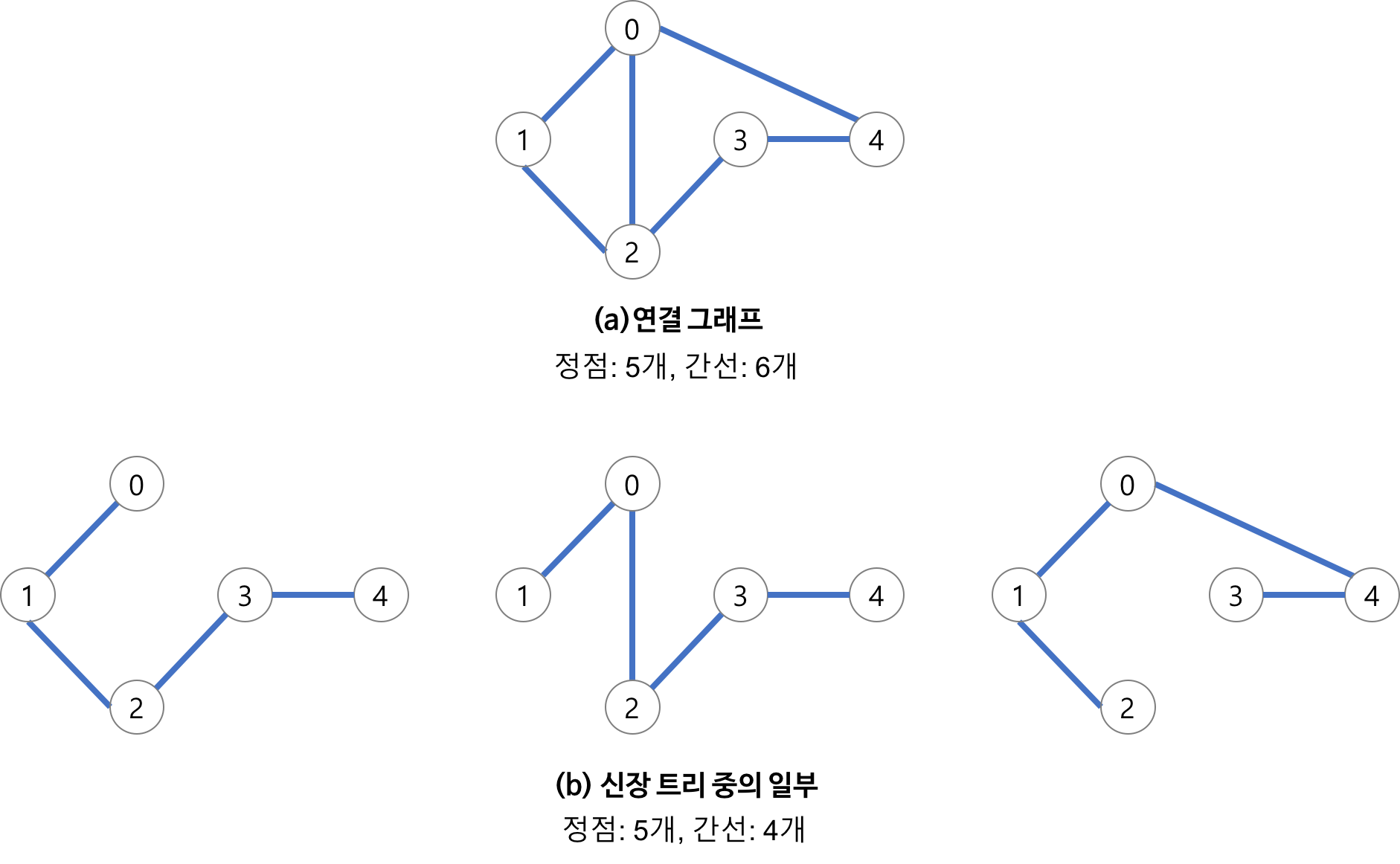
트리의 속성
정점이 N이면 간선의 개수는 N-1개이다.
인접리스트를 트리로 만들때 root노드는 아무거로나 선택해도 답에 지장이 없(었다 지금까지는).
인접리스트를 트리로 전환하기
간선 가중치 없는 무방향 인접리스트를 방향그래프 형태의 트리로 전환해준다.
이렇게 했을때 이점은 parent방향으로 이동하는 간선을 끊어버리기 때문에 순서를 매겨서 루트부터 전 노드 방문하기가 편해진다.
아래 코드에서 treefy()를 재활용하면 된다.이 문제의 답안이기도 하다. 하나의 함수로 패키징하기 위해서 람다(lambda) 함수를 사용했고, 재귀를 가능하게 하기 위해서 std::function을 사용했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#include <bits/stdc++.h>
using namespace std;
#define REP(i,n) for(int i=0;i<(int)(n);i++)
using vi = vector<int>;
const int INF = (int)1e9, MAXN = 100001;
//무방향그래프를 인풋으로 받아, 특정 정점을 루트를 가지는 방향그래프(트리)로 만들어준다.
struct result { vector<vi> tree; int root; vi parent, level; };
result treefy(vector<vi>& adj_list, int root = -1, bool base1 = false) {
int max_v = (int)adj_list.size();
vector<vi> tree(max_v);
if (root == -1)
{
//find root(왼쪽이 parent인경우만 성립)
map<int, int> m;
for (int i = (int)base1; i < max_v;i++)
for (auto a : adj_list[i]) m[a]++;
for (int i = (int)base1; i < max_v; i++)
if (m[i] == 0) { root = i; break; }
}
vi parent(max_v), level(max_v);
function<void(int, int,int)> dfs = [&](int node, int par,int lv) {
parent[node]=par,level[node] = lv;
for (auto adj : adj_list[node]) {
if (adj == par) continue; // 부모방향 간선제거
tree[node].push_back(adj);
dfs(adj, node, lv+1);
}
};
dfs(root, -INF, 1);
return { tree, root, parent, level };
}
int N, R, Q, U, V;
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin >> N >> R >> Q;
vector<vi> adj_list(N + 1);
REP(i, N - 1) {
cin >> U >> V;
adj_list[U].push_back(V);
adj_list[V].push_back(U);
}
vector<vi> tree = treefy(adj_list, R).tree;
vi dp(MAXN, INF);
function<int(int)> cnt_sub = [&](int root) {
int& res = dp[root];
if (res < INF) return res;
int sum = 1; for (auto adj : tree[root]) sum += cnt_sub(adj);
return res = sum;
};
cnt_sub(R);
while (Q--) cin >> U, cout << dp[U] << '\n';
return 0;
}
|
cs |
랜덤으로 트리 인풋만들기
디버깅을 하거나 문제를 출제하다보면, 랜덤한 트리를 만들 필요가 있는데, 임의로 간선을 선택하다보면 사이클이 생겨서 잘 안된다.
이럴때 MST구할때 쓰는 크루스칼 알고리즘을 사용하면 간단하게 사이클 없는 트리를 만들 수 있다.
아래는 내가 구현한 코드이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include <bits/stdc++.h>
using namespace std;
#define REP(i,n) for(int i=0;i<(int)(n);i++)
#define REP1(i,n) for(int i=1;i<=(int)(n);i++)
using vi = vector<int>;
using vvi = vector<vi>;
struct union_find {
vi parent;
union_find(int n) {
parent.resize(n + 1);
REP1(i, n)parent[i] = i;
}
int find(int x) {
int ox = x;
while (parent[x] != x) x = parent[x];
return parent[ox] = x;;
}
void uni(int x, int y) {
int xp = find(x), yp = find(y);
parent[yp] = xp;
}
};
int main()
{
int N = 7;
cout << N << '\n';
vvi adj_list(N + 1);
union_find uf(N);
int U, V;
REP(i, N - 1) { // 트리는 반드시 N-1개의 간선을 가진다.
A:
U = rand() % N + 1;
V = rand() % N + 1;
if (uf.find(U) == uf.find(V)) goto A; // 사이클을 가지면 채택하지 않는다.
uf.uni(U, V);
cout << U << ' ' << V << '\n';
adj_list[U].push_back(V);
adj_list[V].push_back(U);
}
return 0;
}
|
cs |
돌리면 아래와 같은 결과를 출력한다.
|
1
2
3
4
5
6
7
|
7
7 2
7 6
4 3
6 1
4 7
1 5
|
cs |
트리 모양을 툴로 확인해보면 다음과 같다.
주어진 그래프가 트리인지 판정하기
일단 트리는 undirected graph에서만 정의되기 때문에, undirected로 한정할 수 있고,
이 문제의 경우처럼, 유니온파인드로 판정하는게 비교적 쉬운 방법인 것 같다.
'Programming > Algorithm' 카테고리의 다른 글
| 기하 (0) | 2020.04.19 |
|---|---|
| 포화이진트리(perfect binary tree), 완전이진트리 (0) | 2020.04.19 |
| 세그멘트 트리 (0) | 2020.04.13 |
| 최소신장트리(MST, Minimum Spanning Tree) (0) | 2020.04.12 |
| 유니온 파인드(Union-Find), 서로소 집합(Disjoint Set) (0) | 2020.04.10 |