
위처럼,
어떤 그래프를 V1과 V2 그룹으로 나누었을때,
그룹내의 정점끼리는 간선이 없고 그룹간 간선만 존재할 때 이분 그래프라고 한다.
주어진 그래프가 이분 그래프인지 판정하기
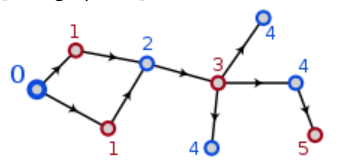
undirected 이면서 모든 두 꼭지점의 연결 경로가 존재하는 연결 그래프(connected graph)인 경우,
아무노드나 잡고, BFS나 DFS로 위처럼 색칠을 해 나가다가 색깔의 conflict 가 있으면 이분 그래프가 아니고, 없으면 이분 그래프로 판정 가능하다.
undirected 이면서 연결 그래프는 아닌경우(위의 그림1도 연결그래프는 아님),
이경우도 단순하게 분리된 각각의 연결 그래프에 대해서 모두 위의 색칠로직을 적용해주면 됨(모든 분리된 그래프가 이분 그래프여야 전체도 이분그래프인걸로 판정)
아래 소스코드 참조. 이 문제의 답안이기도 하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <bits/stdc++.h>
using namespace std;
#define REP(i,n) for(int i=0;i<(int)(n);i++)
enum Color {BLACK, BLUE, RED};
int32_t main()
{
int K; scanf("%d", &K);
while (K--) {
int V, E; scanf("%d%d", &V, &E);
vector<vector<int>> adj_list(V + 1);
while (E--) {
int u, v; scanf("%d%d", &u, &v);
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}
stack<int> qn; REP(i, V)qn.push(i + 1);
vector<int> color(V + 1, BLACK);
bool ans = true;
while (ans == true && qn.empty() == false) {
int n = qn.top(); qn.pop();
if (color[n] == BLACK) color[n] = BLUE;
for (auto adj : adj_list[n]) {
if (color[adj] == BLACK) {
color[adj] = (color[n] == BLUE) ? RED : BLUE;
qn.push(adj);
}
else if (color[adj] == color[n]) {
ans = false;
break;
}
}
}
printf("%s\n", ans ? "YES" : "NO");
}
return 0;
}
|
cs |
directed인경우,
이 경우도 판정 가능한거 같은데, 자세히 알아보진 않았다.
반응형
'Programming > Algorithm' 카테고리의 다른 글
| meet in the middle 알고리즘 (0) | 2022.03.02 |
|---|---|
| 투 포인터 (0) | 2022.03.01 |
| 세그먼트 트리(Segment Tree, 구간트리) (1) | 2020.05.23 |
| 2-SAT(2-CNF Satisfiability Problem) (0) | 2020.05.06 |
| 단절점(Cut Vertex, Articulation Point)과 단절선(Bridge) (0) | 2020.05.03 |
